Khan_Academy_Probability_and_Statistics 05_계산_순열_조합
확률 변수
이산확률 변수 및 연속확률 변수
Random Variables 는 두가지로 구성되어 있다.
1. 이산확률변수
2. 연속확률변수 : any value
이산확률분포의 분산과 표준편차
아산확률분포의 분산 구하기
Var(X) = sigma( (value - avg)^2 * probability)
-> 표준편차는 루트 씌우기
확률변수 합과 차의 분산
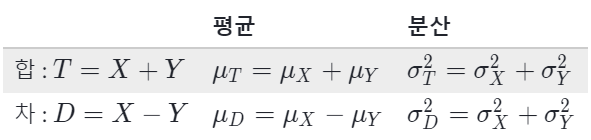
두 확률변수의 합의 평균은 -> 두 확률변수의 각각의 평균을 더하면 됨
E(X+Y) = E(X) + E(Y)
두 확률변수의 합으 분산은 그냥 더하기로 구할 수 없음
Var(X+Y) = Var(X) + Var(Y) -> 불가능
but 두 확률분포의 합의 분산은 증가하게된다.
-> * 두 확률변수가 독립적이라면 두 확률변수의 차의 분산은 두확률분수분산의 합과 같아진다.
독립을 가정하는 10%의 규칙
표본 크기가 모집단의 10%이고 이것을 복원하지 않고 독립을 가정할 수 있다.
작은 표본 크기가 될수록 독립으로 가정하기가 좋아짐 (표본이 클수록 통계적으로는 좋음 ! 작을수록 좋다는 이야기가 아님)
Binompdf와 binomcdf 함수
- Binompdf
이산확률 분포에서 확률이 x인 값이 m번중 n번 나올 확률
binompdf(m,x,n)
(m)C(n) * x^n * (1-x)^(m-n)
- binomcdf
이산확률 분포에서 확률이 x인 값이 m번중 n번 이하가 나올 확률
binomcdf(m,x,n)
베르누이 분포의 평균과 분산
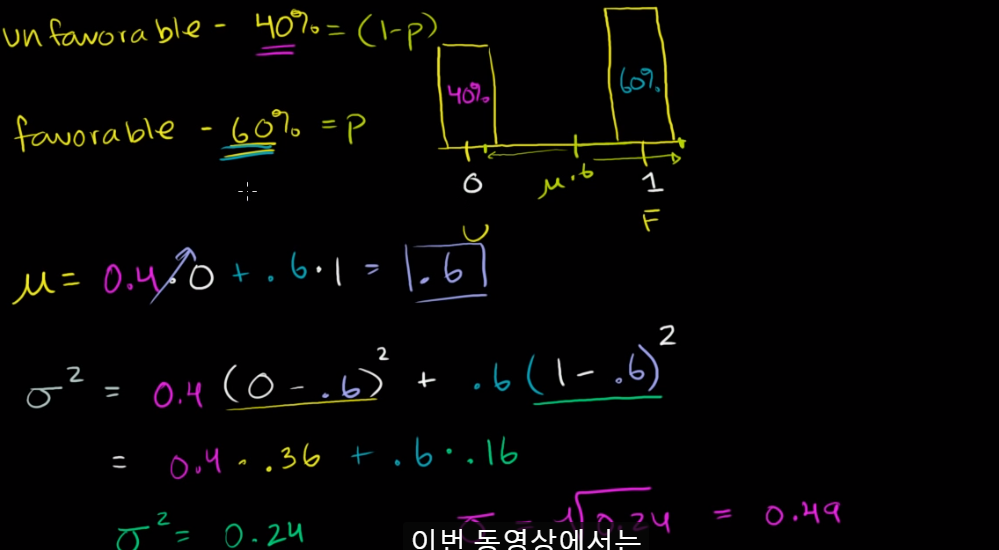
- 베르누이 분포의 평균과 분산 공식
위 사진의 두 분포의 관계를 풀어쓴것
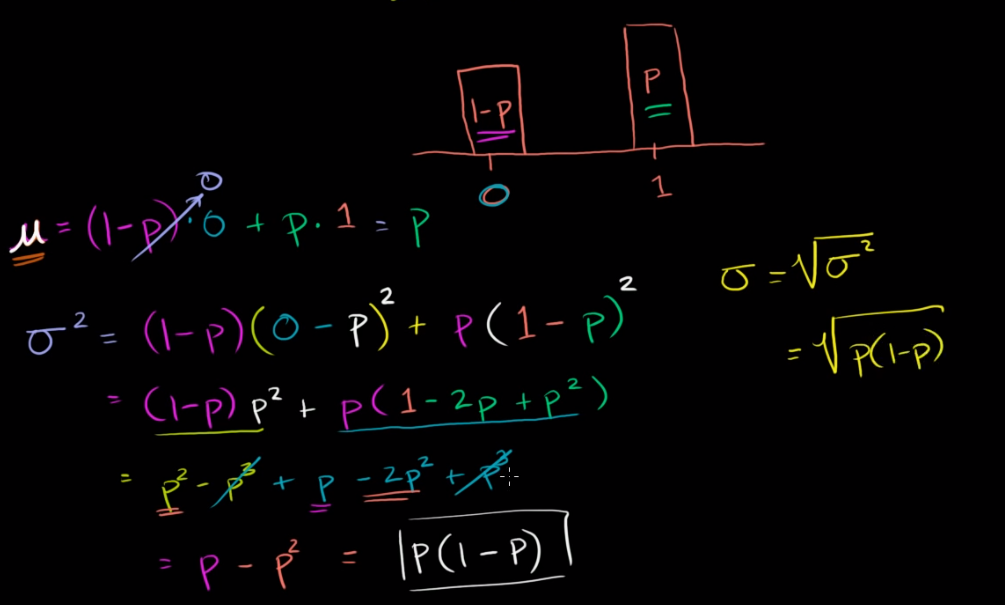
이항변수의 기대값, 분산
### 기하변수(Geometric Random Variable)
독립시행 일정한 확률을 만족하지만 정해진 횟수의 시행겨로가에 대해서는 알수 없는 것
### 큰 수의 법칙
큰 수의 법칙에 따르면 표본평균은 확률변수에 매우 근접 ```